| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 소스코드 줄번호
- unity
- 유니티 머신러닝
- ML-Agents
- c++
- 유니티 Rotate
- 이진트리
- Mathf.Clamp
- eulerAngles
- git-lfs
- 유니티
- 유니티 InputManager
- 코드블럭 테마
- 유니티 시야 가림
- Quaternion.Euler
- 너비 우선 탐색
- Raycast
- LookRotation
- 알고스팟
- 유니티 오브젝트 풀링
- 유니티 ResourceManager
- LFS
- 유니티 Collision
- 유니티 리소스매니저
- 유니티 Vector3
- 오브젝트 풀링
- InputManager
- 깊이 우선 탐색
- LayerMask
- c++ 문자열 자르기
- Today
- Total
무민은귀여워
[그래픽스] 빛 조명 프레넬 효과 본문
조명(lighting)과 음영(shading)은 물체의 입체감과 부피감을 묘사하는 데 큰 도움이 된다. 물론, 일반적으로 조명 모형이 정확할수록 그 계산 비용이 높다. 따라서 사실감과 속도의 균형을 맞추는 것이 중요하다.
재질(material)은 빛이 물체의 표면과 상호작용하는 방식을 결정하는 속성들의 집합이라고 표현할 수 있다. 그러한 속성들의 예로는 표면이 반사, 흡수하는 빛의 색상, 표면 아래 재질의 굴절률, 표면의 매끄러운 정도, 투명도 등이 있다. 재질 속성들을 적절히 지정함으로써 나무나 돌, 유리, 금속, 물 같은 현실 세계의 다양한 표면을 본뜰 수 있다.
법선벡터
면 법선(face normal)은 다각형이 면한(facing; 향한, 바라보는) 방향을 나타내는 단위벡터로, 다른 식으로 표현하면 다각형의 모든 점에 수직인 단위벡터이다.

표면법선(surface normal)은 표면의 한 점의 접평면(tangent plane)에 수직인 단위벡터이다.

주변광, 확산광, 반사광
주변광(ambient light; 물체 주변에 있는 모든 간접광을 근사하는 가상의 빛) : 빛의 근원은 있지만 방 혹은 장면 주위에서 반사되어 들어오기 때문에 방향이 없는 광선이다. ambient light에 의해서 조명되는 물체는 전체적으로 모든 방향으로부터 빛이 비추어진다. 물체를 회전시켜도 ambient light에 의해 색이 변하지 않는다. 즉, 방향을 갖고 있지 않은 ambient light가 그 물체를 비추고 있었기 때문에, 어느 각도에서도 같은 색으로 보여지는 것이다.
확산광(diffuse light) : 특정한 방향으로 비춰지지만, 그 빛의 반사는 여러 방향으로 이루어진다. 빛이 골고루 반사된다 하더라도, 물체를 비스듬히 비출 때보다 바로 위에서 비출 때가 물체 표면을 더 밝게 보인다. 예로써 형광등의 빛이나 오후에 창을 통해 들어오는 햇빛을 생각하면 된다.
반사광(specular light) : 역시 방향을 가지는 빛이다. 하지만 사방으로 빛을 반사시키는 diffuse light 와는 달리 특정 방향으로만 뚜렷하게 반사시킨다. 강한 specular light이 물체에 닿으면 그 표면에 spot이 생기는데 이것을 specular highlight라고 한다.
프레넬 효과
굴절률이 다른 두 재질 사이에 있는, 법선이 n인 평평한 표면을 생각해 보자. 그 표면을 경계로 굴절률이 달라지므로, 표면에 도달한 빛의 일부는 굴절되고 나머지는 반사된다.
프레넬 방정식은 입사광 중 반사되는 빛의 비율인 R (여기서 0 <= R <= 1)를 수학적으로 표현한 것이다.
에너지 보존 법칙에 의해, 반사된 빛의 양이 R이면 굴절된 빛의 양은 (1 - R)이다. 빛의 색에 따라 반사의 양이 다르므로, 실제 응용에서 R의 값은 스칼라가 아니라 3차원 벡터이다.
반사된 빛의 양은 매질에 따라(빛을 더 잘 반사하는 재질이 있다), 그리고 법선 벡터 n과 빛 벡터 L 사이의 각도 θ에 따라 달라진다. 완전한 프레넬 방정식은 상당히 복잡하기 때문에 실시간 렌더링에서 그대로 사용하는 경우는 드물다. 대신 다음과 같은 슐릭 근사(schlick approximation)가 흔히 쓰인다.
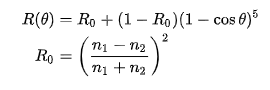
주목할 점은 θ가 90에 가까워짐에 따라 반사광의 양도 증가한다는 것이다.
여기서 실제 세계의 예를 하나 살펴보자. 물이 비교적 맑은 잔잔한 연못으로 걸어 들어가서 수십이 50cm인 지점에서 아래를 내려다보면 연못 바닥의 모래와 돌들이 잘 보일 것이다. 이는 주변환경에서 비롯된 빛이 수면에 반사되어 눈으로 들어올 때, 그 반사각 θ가 0에 가까운 작은 값이기 때문이다. 각도가 작으므로 반사광의 양이 적으며, 따라서(에너지 보존 법칙에 의해) 굴절되는 양은 많다. 결과적으로 주변환경의 방해 없이 연못 바닥을 잘 볼 수 있다. 그러나 고개를 들어서 지평선 쪽을 보면 주변 환경이 반사된 모습을 더 많이 보게 된다. 이는 환경에서 비롯된 빛이 눈으로 들어오는 각도 θ가90에가까워져서반사광의양이증가하기때문이다.
이러한 현상을 흔히 프레넬 효과(Fresnel effect)라고 부른다.
프레넬 효과를 간단히 말하면, 반사광의 양은 법선과 빛 벡터 사이의 각도와 재질(R(0))에 의존한다.

'IT > 기타' 카테고리의 다른 글
| Root 모션 (0) | 2021.05.18 |
|---|---|
| 역운동학 (IK : Inverse Kinematics) (0) | 2021.05.18 |
| Readme 파일에 이미지 넣기 (마크다운 이미지) (6) | 2021.05.18 |
| 짐벌락(gimbal lock)과 사원수(쿼터니언, quaternion) (1) | 2021.05.18 |
| memo) redis 패턴으로 데이터 삭제 (0) | 2021.05.17 |



